MJay
알고리즘 시험 준비 - [2/3 Homework] 본문
Homework 2


Find Upper Envelop of the line intersection.
Half-Plane -> Convex Hull using duality between the set of points and a set of lines.
N lines -> N points in the dual plane.
Upper Envelop -> Easier hull of the convex
Using Grahams’s scan algorithm (nlogn)


y축 젤 작은거를 찾는다.
그리고 작은거 기준으로 counter-clockwise 로 되는 걸 찾는다.
이걸 각각의 점에서 한다. 총 8개의 점이 convex hull을 구성하는 걸 알고있기떄문에
각각의 Iteration 별로 한개의 점을 찾으면 되고 그게 O(n)이 걸리니 O(8 *n)이라서 O(n)이다.

We can solve this problem by removing some points such that derive non-convexity. From the current point pi, we investigate the direction of pi → pi+1 → pi+2. (If the indices exceed n, subtract n from them) If the direction is counter-clockwise, then continue. Otherwise, we exclude pi+1. And we check with pi, pi+2, pi+3 again. The algorithm iteratively goes through until we meet the starting point. Therefore, the running time is O(n). For the proof of the correctness, we need to show two things. First of all, it is obviously a convex polygon because we removed every point that derives non-convexity. Second, all the removed points are included in the convex polygon resulted from this algorithm. If not, the direction with the removed point was counter-clockwise. So, the polygon from this algorithm is the convex hull for the given point sets.
이미 정렬이 되어있다. 각 세점끼리 해서 counter-clock-wised 가 되면 continue 하고 아니면 i+1 를 뺴고 i -> i+2 -> i+3 이렇게 하면 된다. 그리고 이게 O(n) 이다. non-convexity가 되는걸 뺏고 그리고 뺸 점들이 convex-polygon 안에 들어있다. 스택에 존재했고 그때는 counter-clockwise 이니까 polygon from this algorithm은 convex hull 이다. 그래서 form a polygon을 한다.

First, let us define a problem that for a convex hull CH, and a point p, finding the two distinct tangent lines that contains the point and cover the convex hull as shown in the figure below. We can figure out the algorithm of time complexity O(logn) by using binary search. For each m, there are only two lines to test for tangency to Q. The result is an O(nlogn) algorithm.
We first test the first case. Consider the dual problem: let S = {s1,s2,···,sn} be the dual lines of P, and let T = {t1,t2,···,tn} be dual lines of Q. Then there exists L in the primary plane such that P is above L and Q are below L if and only if in the dual plane there exists a point x (dual of L) such that x is above all lines in S and x is below all lines in T . This is equivalent to decide whether the intersection of the upper part of all lines in S and the lower part of all lines in T is empty, which can be reduced to the half-plane-intersection problem.
이걸 기억하면 될듯하다
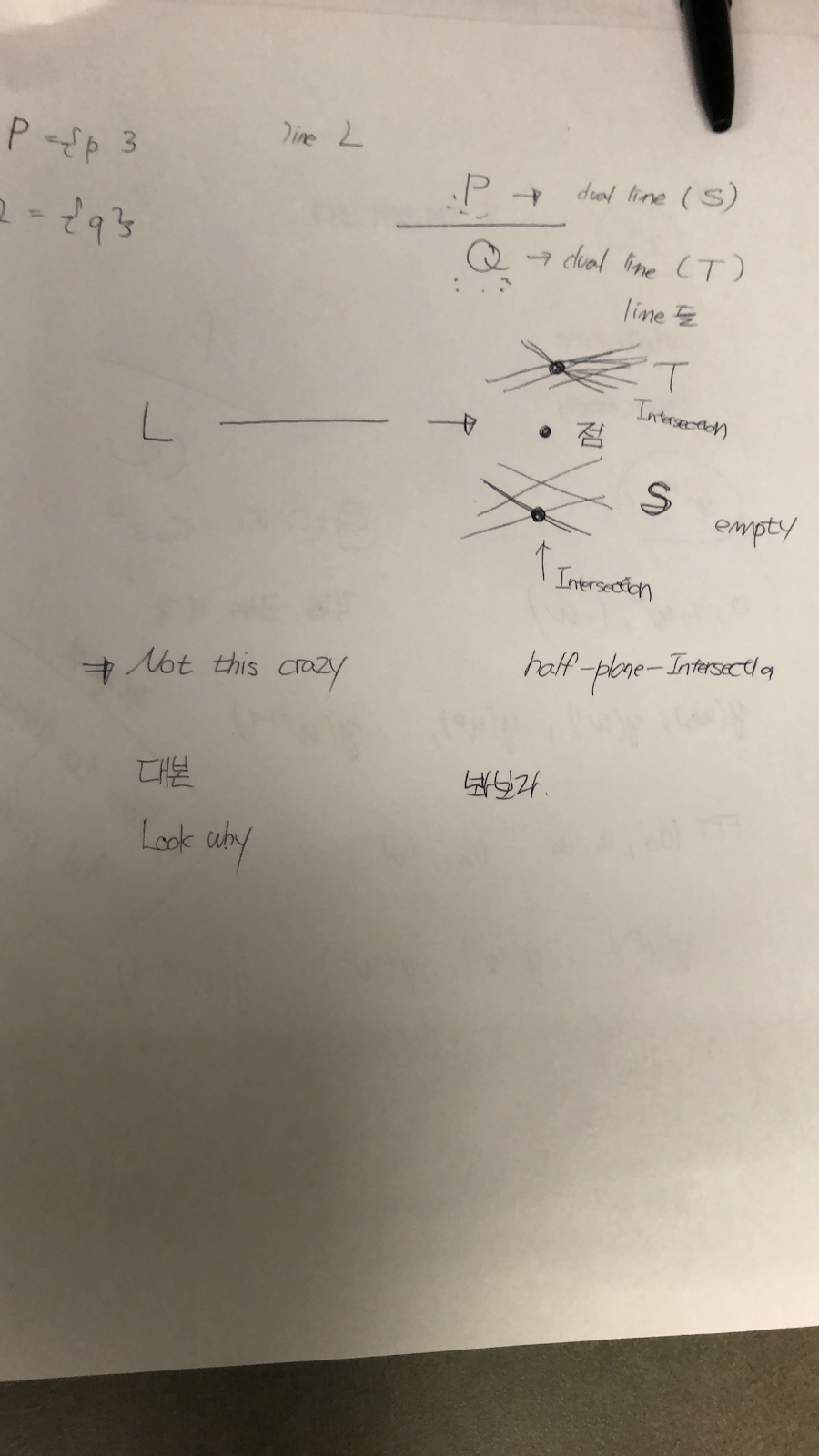
5번은 스킵하기로


각 weight에 값이 있다고 생각하고 다이스트라르 하면 된다.
처음 Node에도 weight를 넣어주면 된다.
7번 문제

정답


c 랑 r를 더하는 거니까 최소화 -> 음수 -> logarithm으로 더한다고 생각하면 된다.
그래서 Bellman-Ford를 해야하는데 음수로 바뀌지 않기 위해 rate 조건이 필요하다
V-1 round 하고 떠 돌릴 경우 V에서 값이 업데이트 되면 음수가 존재하는거인데 즉 그 말이 -log 뭐시기가 0보다 작다는 것이다. 즉 그걸 돌려서 말하면 rate 조건이 필요하다는 것이다.
이렇게 판단을 할수있다.
문제


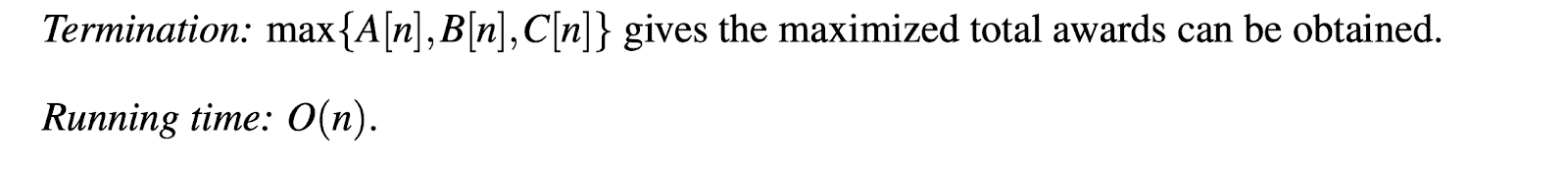

쉬는 거 , hard , easy
쉬는거는 다 전껄로 하면 되고
easy는 쉬는거랑 전에 easy로 하면 되고
hard는 쉬는거 전거랑, easy 전거랑 하면 되겠네 , hard는 쉬는거에 포함이 된다.

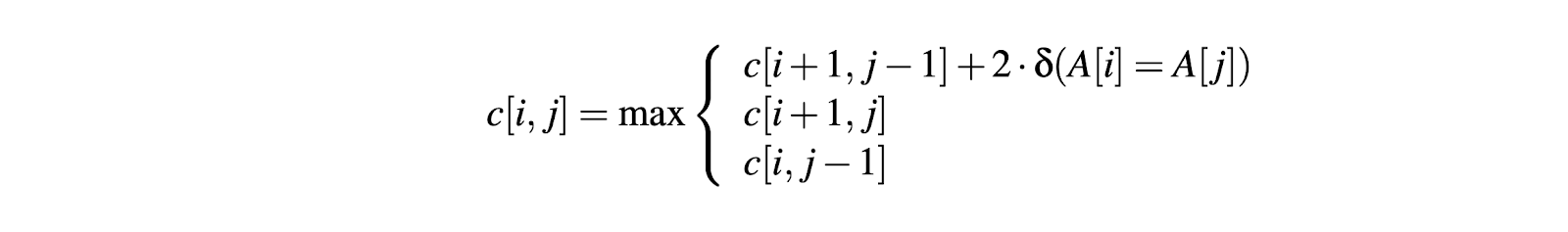


이건 뭐 간단하지 뭐
'PSU > CSE 565 - Algorithm' 카테고리의 다른 글
| 알고리즘 시험 준비 - [10/13 Files] - 2019-09-30 (0) | 2019.10.18 |
|---|---|
| 알고리즘 시험 준비 - [3/3 Homeworks] (0) | 2019.10.18 |
| 알고리즘 시험 준비 - [1/3 Homework] (0) | 2019.10.17 |
| 알고리즘 시험 준비 - [3/3 Quizzes] (0) | 2019.10.17 |
| 알고리즘 시험 준비 - [2/3 Quizzes] (0) | 2019.10.17 |




